정렬 뿌시기
힙정렬, 합병정렬, 퀵정렬
1. 힙 정렬
-
힙은 느슨한 정렬으로 자식은 부모보다 항상 크거나 작도록 정렬한다(최대힙/최소힙)
-
시간복잡도는 O(N * logN) 이다.
-
N : 모든 노드를 대상으로 for문
-
logN : 자식에서 부모로 이진트리를 따라 올라감
-
// maxHeap(data, number) - data : 정렬 대상배열, number : 배열의 크기
// 최대힙 정렬
void maxHeap(int []data, int number){
for(int i=1; i< number; i++){
// 0을 제외한 이유는 비교대상이 자식 노드이므로 루트노드를 제외하였기 때문이다.
int child = i; // 루트노드를 제외하곤 항상 어떤 노드의 자식이다.
while(child > 0){
// (child-1) / 2는 부모 인덱스를 의미한다.
// -1을 하기 싫으면 최상단 루트의 인덱스를 1부터한다.(지금은 0)
int parent = (child - 1) / 2;
// 부모노드값이 자식보다 작으면 바꾼다.
if(data[child] > data[parent]){
int temp = data[parent];
data[parent] = data[child];
data[child] = temp;
}
// 루트노드까지 반복한다.
child = parent;
}
}
}
2. 합병 정렬
-
분할 정복 알고리즘의 종류
-
하나의 큰 문제를 두 개의 작은 문제로 분할한 뒤에 각자 계산한 뒤에 합치는 방법!
-
개념이 이해 안된다면 다음 링크로 가서 영상을 보면 진짜 쉽게이해된다.(합병/병합정렬 참고링크)
[5, 3, 2, 4, 9] 배열 합병 정렬 하기
-
분할
[5, 3, 2] [4, 9]
[5, 3] [2] [4] [9]
[5] [3] [2] [4] [9] : 기저조건에 해당
-
Conquer
- [5] [3]
5와 3을 비교한다
[ ?, ?] -> [3, ?]
나머지 5 입력
[3, 5]
- [3, 5] [2]
3과 2를 비교한다
[?, ?, ?] -> [2, ?, ?]
나머지 3, 5 입력
[2, 3, 5]
- [4] [9]
4와 9를 비교한다
[?, ?] -> [4, ?]
나머지 9 입력
[4, 9]
- [2, 3, 5] [4, 9]
2와 4를 비교한다.
[?, ?, ?, ?, ?] -> [2, ?, ?, ?, ?]
3과 4를 비교한다.
[2, 3, ?, ?, ?]
5와 4를 비교한다.
[2, 3, 4, ?, ?] … [2,3,4,5,9] 완성
-
-
시간복잡도 (참고링크)
항상 반으로 나누기 때문에 logN이다.
합치는 순간에 정렬을 할때 수행시간은 N이다.
부분 집합들은 정렬되어 있는 상태이므로 정렬되어 있는 두개를 합치는 시간 복잡도는 O(N)이다.
int[] arr = {5, 3, 2, 4, 9};
mergeSort(arr, 0, arr.length-1);
void mergeSort(int[] arr, int start, int end){
if(start < end){
int middle = (start + end) / 2;
mergeSort(arr, start, middle);
mergeSort(arr, middle+1, end);
merge(arr, start, middle, n);
}
}
void merge(int[] arr, int start, int middle, int end){
int i = start;
int j = middle + 1;
int k = start;
int temp[] = new int[(end-start)+1]; //합쳐진 결과를 저장하는 임시변수
int idx = 0;
// 작은 순서대로 배열에 삽입
while(i <= middle && j <= end){
if(arr[i] <= arr[j]){
temp[idx++] = arr[i++];
} else {
temp[idx++] = arr[j++];
}
}
// 한쪽 인덱스 범위를 초과 했을때 나머지 한쪽의 값들을 전부 temp 배열에 추가
if(i > middle){
// 왼쪽은 전부 정렬된 상태 오른쪽 나머지 temp 배열에 추가
for(int temp=j; temp <= end; temp++){
temp[idx++] = arr[temp];
}
} else {
// 오른쪽은 전부 정렬된 상태 왼쪽 나머지 temp 배열에 추가
for(int temp=i; temp <= middle; temp++){
temp[idx++] = arr[temp];
}
}
for(int val=start; val <= end; val++){
arr[val] = temp[val-start];
}
}
3. 퀵정렬
-
분할정복 알고리즘의 하나!
-
과정 설명 (참고링크)
-
리스트 안에 있는 한 요소를 선택한다. 이렇게 고른 원소를 피벗(pivot)이라 한다.
-
피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗 왼쪽으로
피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮긴다.
-
피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬한다.
-
분할된 부분 리스트에 대하여 순환 호출을 이용하여 정렬을 반복한다.
-
부분 리스트에서도 다시 피벗을 정하고
피벗을 기준으로 2개의 부분리스트로 나누는 과정을 반복한다.
-
-
부분 리스트들이 더이상 분할이 불가능할 때까지 반복한다.
- 리스트 크기가 0이나 1이 될 때까지 반복한다.
-
4. 퀵 정렬의 구체적인 개념
-
하나의 리스트를 피벗(pivot)을 기준으로 두 개의 비균등한 크기로 분할하고
분할된 부분 리스트를 정렬한 다음 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트로 만든다.
-
퀵 정렬은 다음 단계들로 이루어진다.
-
분할(Divide) : 입력 배열을 피벗을 기준으로 비균등하게 2개의 부분 배열로 분할한다.
-
정복(Conquer) : 부분 배열을 정렬한다.
부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다 시 분할 정복 방법을 적용한다.
-
결합(Combine) : 정렬된 부분 배열들을 하나의 배열에 합병한다.
순환 호출이 한번 진행될 때마다 최소 하나의 원소(피벗)는 최종 위치가 정해지므로
이 알고리즘은 반드시 끝남을 보장할 수 있다.
-
-
퀵정렬의 시간복잡도
-
최선의 경우
-
순환 호출의 깊이
레코드 개수 n이 2의 거듭 제곱이라 가정했을때(n = 2^k)
n=2^3의 경우 2^3 > 2^2 > 2^1 > 2^0 순으로 줄어들어 순환 호출의 깊이가 3임을 알 수 있다.
이를 일반화하면 n=2^k 인경우 k = logN 임을 알 수 있다.
-
각 순환 호출 단계의 비교 연산
각 순환 호출에서는 전체 리스트의 값을 피벗(pivot)과 비교해야 하므로 평균 n번의 비교가 이루어짐
-
O(nlogn)
-
-
최악의 경우
-
리스트가 불균형하게 나누어지는 경우
-
순환 호출의 깊이가 레코드의 개수 n이 2의 거듭제곱이라 가정했을때(n = 2^k)
순환 호출의 깊이는 n 임을 알 수 있다.
-
비교 연산은 피벗과 전체 리스트가 값을 비교하므로 평균 n번 이루어진다.
-
따라서 n*n = O(n^2)
-
-
-
퀵정렬 예제 [5, 3, 8, 4, 9, 1, 6, 2, 7]
[Partition]
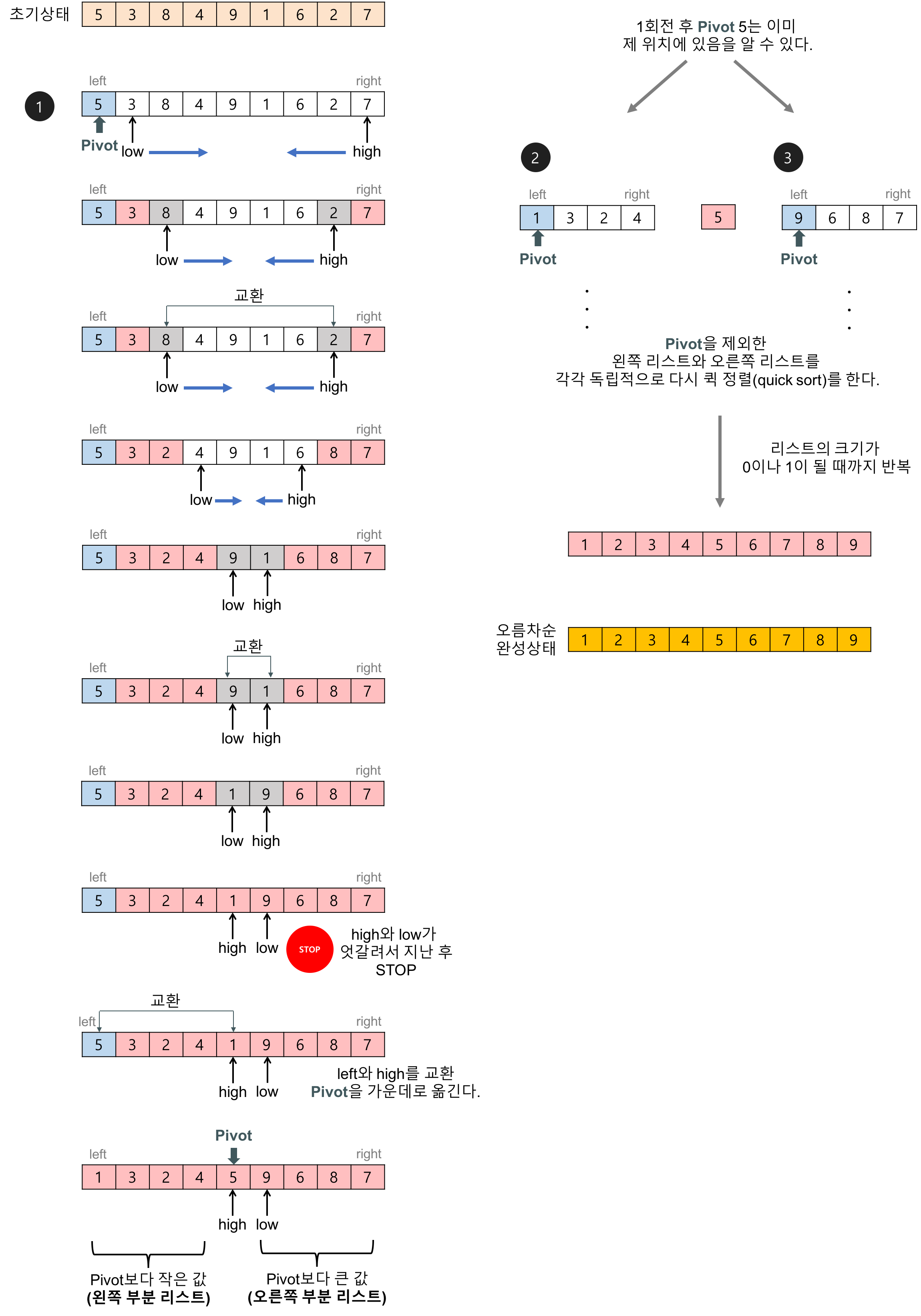
-
구현
int[] list = new int[]{5, 3, 8, 4, 9, 1, 6, 2, 7};
quick_sort(list, 0, list.length-1);
void quick_sort(int[] list, int left, int right){
// 정렬 범위가 2개 이상의 데이터이면
if(left < right) {
// partition 함수를 호출하여 피벗을 기준으로 비균등 분할
int q = partition(list, left, right); // q : 피벗의 위치
// 피벗은 제외한 2개의 부분 리스트를 대상으로 순환 호출
quick_sort(list, left, q-1);
quick_sort(list, q+1, right);
}
}
int partition(int []list, int left, int right){
int pivot, temp;
int low, high;
low = left;
high = right+1;
pivot = list[left];
do {
// list[low]가 피벗보다 작으면 계속 low를 증가
// low는 left+1에서 시작(left는 피벗)
// pivot이 list[left]보다 큰 값에서 멈춘다.
do {
low++;
} while(low <= right && list[low] < pivot);
// list[high]가 피벗보다 크면 계속 high를 감소
// high는 right에서 시작
// pivot이 list[high]보다 작은 값에서 멈춘다.
do {
hight--;
} while(high >= left && list[high] > pivot);
// low와 high가 교차하지 않았으면 list[low]와 list[high] 교환
if(low < high){
swap(list[low], list[high]);
}
} while (low < high)
swap(list[left], list[high]);
return high;
}